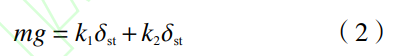引言

鉛冷快堆（LFR）是第四代核能國際論壇（GIF）確立的6種第四代反應(yīng)堆之一[1]。螺旋盤管型直流蒸汽發(fā)生器結(jié)構(gòu)緊湊，換熱能力強，因此國際上一些鉛冷快堆選擇其作為主換熱器[2-3]。流致振動現(xiàn)象廣泛存在于蒸汽發(fā)生器中，從而導(dǎo)致微動磨損現(xiàn)象出現(xiàn)，嚴(yán)重時將導(dǎo)致蒸汽發(fā)生器傳熱管破裂事故，威脅反應(yīng)堆安全[4]。國內(nèi)外對蒸汽發(fā)生器傳熱管的流致振動問題越發(fā)關(guān)注，一些學(xué)者針對螺旋盤管管束開展流致振動實驗與數(shù)值研究[5-6]，研究發(fā)現(xiàn)增加上下游管束將增加振動頻率，但是會導(dǎo)致振動響應(yīng)相對減少。Jung等人[7-8]研究了曲率管面內(nèi)與面外的振動特性，發(fā)現(xiàn)了面外方向上出現(xiàn)了倍頻現(xiàn)象，同時不穩(wěn)定區(qū)域的大小也會隨流速的增大而增大。管內(nèi)流動所產(chǎn)生的振動多為較高頻率的微動，這類振動更易誘發(fā)微動磨損[9-10]。因此，很多學(xué)者針對螺旋盤管內(nèi)流致振動開展了一系列研究。Tang等[11]建立了彎曲微管的振動理論模型，該模型同時考慮面內(nèi)與面外的振動，并基于拉格朗日非線性軸向應(yīng)變來獲得管內(nèi)流體流動所產(chǎn)生的靜變形。

Ibrahim[12]認為管內(nèi)流致振動的本質(zhì)上是由于慣性力、彈性力以及離心力相互作用導(dǎo)致的。目前針對螺旋盤管內(nèi)流致振動相關(guān)研究主要關(guān)注盤管的振動響應(yīng)特征，而管內(nèi)流體流動狀態(tài)對振動響應(yīng)間的內(nèi)在聯(lián)系尚未厘清，無法提出更具普適性的振動機制。因此亟需開展相關(guān)研究，探究管內(nèi)流體流動狀態(tài)對振動響應(yīng)的影響機制。本研究基于激光多普勒測量技術(shù)，開展螺旋盤管內(nèi)單相流致振動實驗，獲得振動響應(yīng)實驗數(shù)據(jù)，結(jié)合模態(tài)分析，探究沿面內(nèi)及面外的振動響應(yīng)特性，明晰了影響螺旋盤管振動響應(yīng)的關(guān)鍵因素，揭示了管內(nèi)流體對振動響應(yīng)的影響機制。本實驗可為螺旋盤管內(nèi)流致振動研究提供參考，并可為后續(xù)管內(nèi)兩相流致振動研究提供支撐。

1、實驗方法

1.1實驗回路

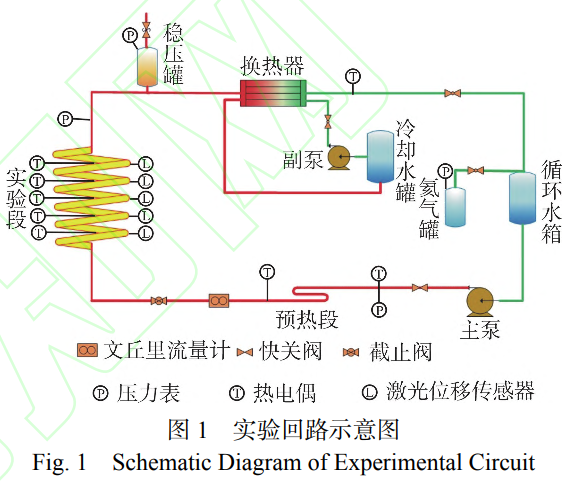
實驗回路示意圖，如圖1所示。實驗回路由一次側(cè)實驗回路與二次側(cè)實驗回路組成。一次測實驗回路由主泵、預(yù)熱段、實驗段及管殼式換熱器等主要部件組成。二次側(cè)實驗回路由冷卻水箱、冷卻水主泵及冷卻塔組成，為一次側(cè)實驗回路提供熱阱。實驗工質(zhì)為去離子水，實驗中，去離子水由主泵流出經(jīng)預(yù)熱段進入實驗段，然后流入管殼式換熱器，最后流回主泵，形成閉式循環(huán)。實驗中，主泵產(chǎn)生的熱量會使得回路中去離子水溫度上升，改變?nèi)ルx子水粘度從而影響實驗結(jié)果，因此需要經(jīng)由管殼式換熱器帶走額外熱量，確保實驗過程中去離子水溫度穩(wěn)定。此外，主泵運行時會產(chǎn)生振動，影響實驗段振動響應(yīng)特性。基于前期實驗經(jīng)驗，實驗段與實驗回路間使用金屬軟管連接，以避免主泵遠場激勵的影響。

1.2實驗本體

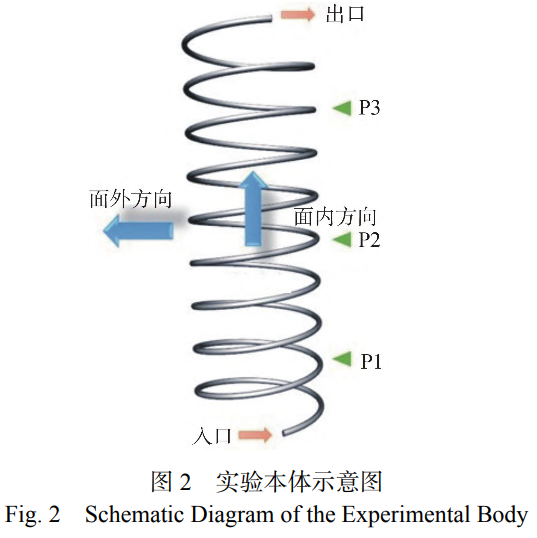
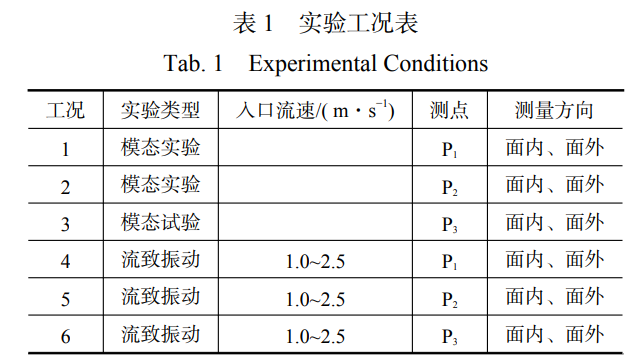
實驗本體示意圖，如圖2所示。實驗本體主要參數(shù)如表1所示。實驗本體材質(zhì)為316L不銹鋼，螺旋直徑與管道直徑比為22.5，螺距為100mm，高度為900mm。實驗本體兩端布置約束裝置，以線面接觸的方式進行固定約束。

1.3測量方法

1.3.1測量儀器　實驗本體入口布置有文丘里流量計，用于測量入口流量，誤差為±0.067%。實驗本體進出口裝有T型鎧裝熱電偶，用于測量實驗本體進出口流體溫度，精度為I級精度。實驗本體振動響應(yīng)特性由激光位移傳感器測量得到，該儀器基于激光多普勒效應(yīng)測量物體振動，位移分辨率為1.28nm，位移重復(fù)精度為1nm，最大速度量程為4500mm/s，采集頻率最大可達2.5MHz。

1.3.2數(shù)據(jù)處理方法　振動位移實驗結(jié)果用均方根（RMS）方法處理。本實驗基于傅里葉變換將時域信號變換為頻域信號。

1.4實驗工況

本研究開展實驗研究包括模態(tài)實驗與流致振動實驗，其中模態(tài)實驗基于力錘敲擊法開展，流致振動實驗旨在探究不同入口流速對螺旋盤管振動響應(yīng)的影響。測點P1高度為200mm、測點P2高度為500mm、測點P3高度為800mm。實驗工況表見表1。

2、實驗結(jié)果與分析

2.1模態(tài)分析

螺旋盤管的特殊結(jié)構(gòu)導(dǎo)致其面內(nèi)固有頻率與面外固有頻率存在差異，影響振動特性。通過開展模態(tài)實驗，獲得螺旋盤管面內(nèi)與面外固有頻率，結(jié)合靜力學(xué)分析厘清質(zhì)量效應(yīng)對振動特性的影響規(guī)律，從而為管內(nèi)單相流致振動響應(yīng)分析提供參考。螺旋盤管各測點處面內(nèi)方向固有頻率均為8.7Hz，各測點處面外方向固有頻率均為8.2Hz。本實驗所用螺旋盤管剛度結(jié)構(gòu)對稱，因此各層盤管固有頻率相同。由于螺旋盤管沿面內(nèi)、面外方向剛度不同，因此沿面內(nèi)、面外方向存在不同固有頻率。為進一步明晰螺旋盤管振動特性，需要結(jié)合靜力學(xué)分析探究質(zhì)量效應(yīng)對固有頻率的影響。根據(jù)力學(xué)分析，可將單層盤管在面外方向上簡化為等效具有等效質(zhì)量自由振動彈簧系統(tǒng)，其固有頻率表達式為：

式中，ω_n為系統(tǒng)固有頻率：k為系統(tǒng)剛度；m為系統(tǒng)質(zhì)量。由表達式可知在面內(nèi)向上固有頻率僅與自身質(zhì)量與剛度有關(guān)。在面內(nèi)方向上，需將單層盤管簡化為并聯(lián)彈簧系統(tǒng)，同時還需考慮重力所致靜變形的影響，受重力影響的并聯(lián)彈簧系統(tǒng)靜變形為：

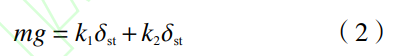
式中，δ_st為系統(tǒng)靜態(tài)變形量；k₁和k₂為并聯(lián)彈簧剛度；g為重力加速度。結(jié)合運動方程推導(dǎo)可得并聯(lián)彈簧系統(tǒng)固有頻率表達式：

由式（5）可知，在螺旋盤管面內(nèi)方向上固有頻率受靜變形影響，這意味每層盤管面內(nèi)方向的振動特性不僅受自身重力影響還會受相鄰盤管推力與拉力影響。

2.2單相流致振動實驗

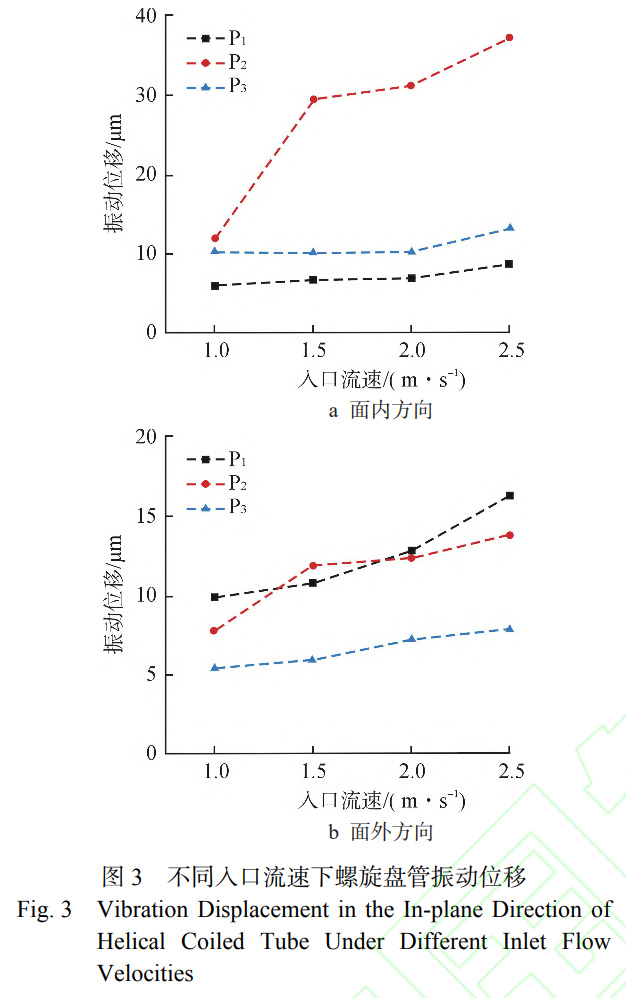
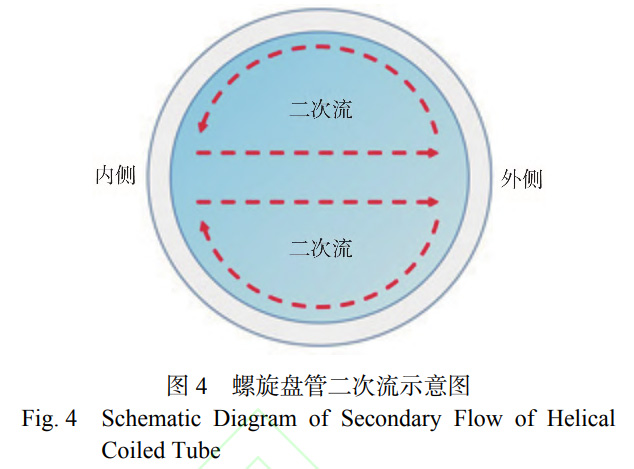
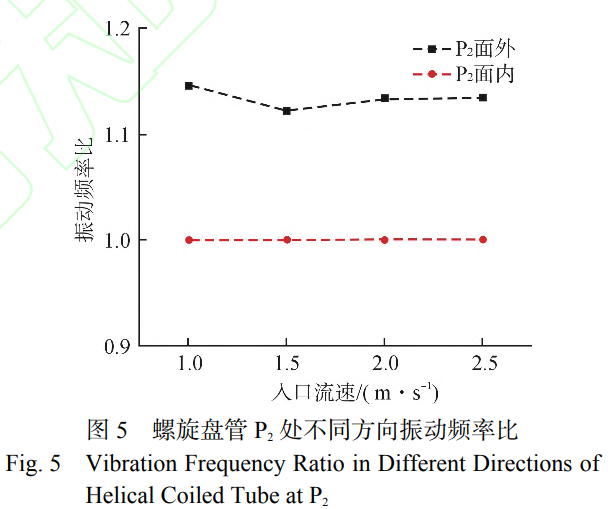
通過開展不同入口流速下管內(nèi)單相流致振動實驗，獲得螺旋盤管各測點振動響應(yīng)實驗數(shù)據(jù)，結(jié)合模態(tài)分析結(jié)果，分析其振動規(guī)律與影響因素。螺旋盤管各測點面內(nèi)方向振動位移如圖3所示。由圖3a可知，螺旋盤管面內(nèi)方向振動位移隨入口流速增加而增加，其中盤管中部（P2測點）測點處振動位移隨入口流速的變化率約為16.9μm·（m·s^?1）^?1，遠高于其他測點，其中P1處振動位移變化率約為1.8μm·（m·s^?1）^?1，P3處振動位移變化率約為1.9μm·（m·s^?1）^?1。由此可見螺旋盤管兩端固支對振動位移具有明顯的約束效果。由圖3b可知，各測點面外方向振動位移演變規(guī)律與面內(nèi)方向有明顯差異。一方面，各測點振動位移變化率相近。另一方面，并未出現(xiàn)螺旋盤管中部振動位移明顯高于兩端的分布特征，P3處振動位移最小，P1與P2處振動位移相近，且在入口流速達到2.5m/s時P1處振動位移更大。導(dǎo)致上述現(xiàn)象的原因是螺旋盤管內(nèi)特殊的流體流動狀態(tài)，受離心力影響螺旋盤管內(nèi)存在二次流動，當(dāng)二次流動激勵管壁時會產(chǎn)生振動響應(yīng)。管內(nèi)二次流示意圖，如圖4所示。二次流形成的根本原因在于流體在螺旋盤管內(nèi)流動受到離心力影響，沿內(nèi)側(cè)至外側(cè)方向移動導(dǎo)致。由此可知，當(dāng)管內(nèi)湍流度較強時，管內(nèi)流體速度分布更加不均勻，從而產(chǎn)生更強的二次流動。在本次實驗中，實驗本體入口為螺旋盤管下端，當(dāng)流體自下而上流過盤管時，受重力與流動摩擦影響，流體湍流強度逐漸下降，從而導(dǎo)致二次流動強度減弱，進而導(dǎo)致振動位移減小。因此，在螺旋盤管面外方向上振動位移隨高度增加而減小，而P1與P2處振動位移相近是受支承約束影響導(dǎo)致。為進一步揭示面內(nèi)與面外方向的振動響應(yīng)機制，需要結(jié)合頻域分析。通常，當(dāng)結(jié)構(gòu)振動頻率與固有頻率接近時，即認為振動響應(yīng)發(fā)生鎖定現(xiàn)象。螺旋盤管P2處，面內(nèi)與面外方向振動頻率比如圖5所示。

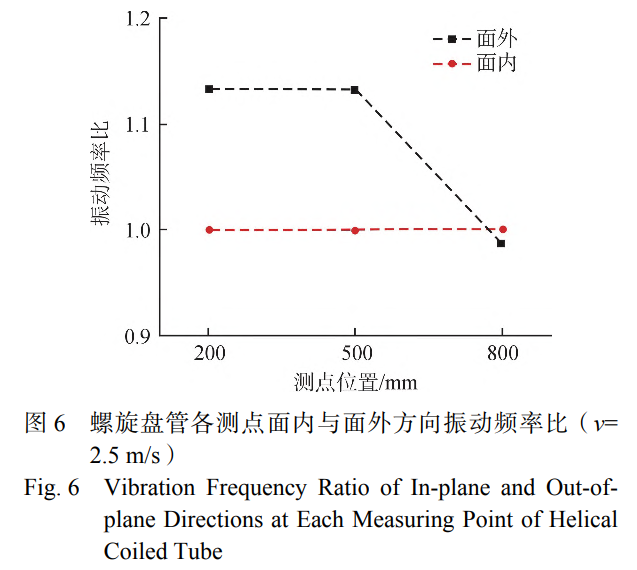
由圖5可知，在面內(nèi)方向上振動頻率比均為1并不隨入口流速變化，出現(xiàn)振動鎖定現(xiàn)象。而面外方向上振動頻率比均超過1，未發(fā)生振動鎖定。2.5m/s入口流速下，螺旋盤管各測點面內(nèi)與面外方向振動頻率比如圖6所示。由圖6可知，在面內(nèi)方向上不同測點的振動頻率比均為1，出現(xiàn)振動鎖定現(xiàn)象。而在面外方向上各測點均為出現(xiàn)振動鎖定。結(jié)合圖5與圖6可知，螺旋盤管在面內(nèi)方向上極易出現(xiàn)振動鎖定現(xiàn)象，這意味著在面內(nèi)方向上所受激勵更接近于隨機激勵，其振動機制為管內(nèi)流體的湍流脈動。

而在面外方向上振動頻率與固有頻率存在一定差異，因此推測面外方向振動響應(yīng)與管內(nèi)流體流動狀態(tài)具有相關(guān)性。為驗證上述分析，需結(jié)合頻譜進行進一步分析。螺旋盤管P2處不同方向頻譜如圖7所示。

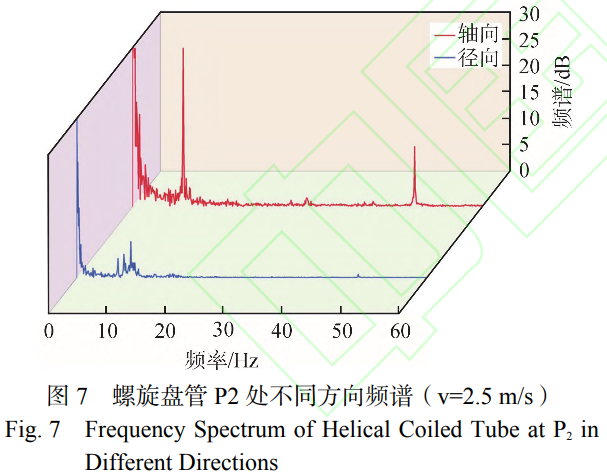
圖7中紅色曲線為面內(nèi)方向振動頻譜，其在固有頻率（8.7Hz）附近的頻率帶寬較窄，僅存在8.7Hz的主要振動頻率。由此可知，在面內(nèi)方向上主要振動機制為管內(nèi)流體的隨機激勵。根據(jù)面外方向頻譜可知，即圖中藍色曲線，其在固有頻率（8.2Hz）附近存在較寬的頻帶，6.7~11.5Hz，具有多個明顯的振動頻率，包括7.1Hz、8.1Hz和9.3Hz。由此可知，在面外方向上振動響應(yīng)與管內(nèi)流體流動狀態(tài)相關(guān)，結(jié)合前文對二次流分析可知，管內(nèi)二次流動為誘發(fā)面外方向振動的主要機制。為驗證上述結(jié)論，需結(jié)合不同沿高度方向上不同測點頻譜數(shù)據(jù)，假設(shè)管內(nèi)二次流動強度或單位時間內(nèi)的循環(huán)次數(shù)隨高度的增加而減少，則螺旋盤管面外方向的振動頻率也將隨高速的增加而減少。螺旋盤管不同測點面外方向頻譜如圖8所示。

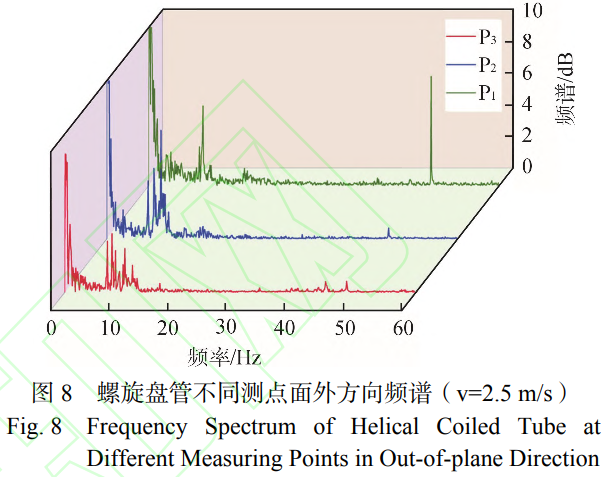
由圖8可知，隨著測點高度的增加，面外方向主振頻率逐漸減小，由9.3Hz減小至8.1Hz，同時主振頻率附近的頻帶呈現(xiàn)出展寬現(xiàn)象，并出現(xiàn)多個明顯的振動頻率。隨著高度的增加，管內(nèi)流體流速不均勻程度加劇，從而導(dǎo)致二次流流動狀態(tài)不穩(wěn)定，進而展寬振動頻帶形成多個明顯振動頻率。綜上所述，在螺旋盤管面外方向上，管內(nèi)二次流動是影響振動響應(yīng)的主要機制。

3、結(jié)論

本研究基于激光多普勒測振技術(shù)，開展螺旋盤模態(tài)實驗與管內(nèi)單相流致振動實驗，獲得振動特性與振動響應(yīng)，探究了螺旋盤管振動響應(yīng)演變規(guī)律，揭示了兩種振動機制，其主要結(jié)論如下：

（1）螺旋盤管在沿面外方向上振動特性受自身質(zhì)量影響，在面內(nèi)方向上同時受所受靜力與質(zhì)量影響。

（2）螺旋盤管面內(nèi)方向振動位移受支承約束影響明顯，而在面外方向上則主要受管內(nèi)流體的二次流強度影響。

（3）螺旋盤管面內(nèi)方向上的主要振動機制為管內(nèi)流體隨機激勵，在面外方向上主要振動機制為管內(nèi)二次流動。

參考文獻：

[1]韓金盛，劉濱，李文強. 鉛冷快堆研究概述 [J]. 核科 學(xué)與技術(shù)，2018, 6(3): 87-97.

[2] CIONCOLINI A, SANTINI L. Two-phase pressure drop prediction in helically coiled steam generators for nuclear power applications[J]. International Journal of Heat and Mass Transfer, 2016, 100: 825-834.

[3] HARDIK B K, PRABHU S V. Heat transfer distribution in helical coil flow boiling system[J]. International Journal of Heat and Mass Transfer, 2018, 117: 710-728.

[4]JO J C, JHUNG M J. Flow-induced vibration and frettingwear predictions of steam generator helical tubes[J]. Nuclear Engineering and Design, 2008, 238(4): 890-903.

[5]YUAN H M, SOLBERG J, MERZARI E, et al. Flowinduced vibration analysis of a helical coil steam generator experiment using large eddy simulation[J]. Nuclear Engineering and Design, 2017, 322: 547-562.

[6] PAI?DOUSSIS M P, LI G X. Pipes conveying fluid: a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204.

[7] JUNG D, CHUNG J. In-plane and out-of-plane motions of an extensible semi-circular pipe conveying fluid[J]. Journal of Sound and Vibration, 2008, 311(1-2): 408- 420.

[8] JUNG D, CHUNG J, MAZZOLENI A. Dynamic stability of a semi-circular pipe conveying harmonically oscillating fluid[J]. Journal of Sound and Vibration, 2008, 315(1-2): 100-117.

[9]DELGADO M. An experimental study on flow-induced vibration of a single and adjacent tubes within a model helical coil heat exchanger[D]. College Station: Texas A&M University, 2021.

[10] PA?DOUSSIS M P. Fluidelastic vibration of cylinder arrays in axial and cross flow: state of the art[J]. Journal of Sound and Vibration, 1981, 76(3): 329-360.

[11] TANG M, NI Q, WANG L, et al. Nonlinear modeling and size-dependent vibration analysis of curved microtubes conveying fluid based on modified couple stress theory[J]. International Journal of Engineering Science, 2014, 84: 1-10.

[12] IBRAHIM R A. Overview of mechanics of pipes conveying fluids —Part I: fundamental studies[J]. Journal of Pressure Vessel Technology, 2010, 132(3): 034001.

相關(guān)鏈接